CSCI 150 - Lab 8 - Fractal Recursion

CSCI 150 - Lab 8
Fractal Recursion

Overview

Certain elements of mathematics can be naturally described by recursion, as we saw with the factorial function. Today, we will look into the mathematics of fractals and how some of their properties can be described with recursion.

Materials

Turtle module

Fractals

We will be using Python's Turtle module to draw fractals such as Sierpinski's Triangle, the Koch Snowflake, and the Dragon Curve. Fractals have also been employed for modeling natural phenomena, most especially plants.

To access the Turtle module and define a turtle, you can use the following lines of code:

import turtle
t = turtle.Turtle()

By calling methods on the variable t, we can make the turtle navigate around the screen and draw lines. (If you want to know why it is called a "turtle", you can read about turtles and Logo and Seymour Papert.)

Some turtle commands you might find useful:

movement around the screen: t.forward(n) and t.back(n) will move the turtle forward or backwards n pixels in the current direction. t.goto(x, y) will go to a particular location on the screen.
changing direction: t.right(d), t.left(d) will turn the turtle left or right by d degrees.
draw a dot on the screen of a certain size: t.dot(size)
put the pen down or pick the pen up: t.penup(), t.pendown()
change the turtle's speed: t.speed(s), where 1 = slowest and 10 = fastest

There are lots of other turtle commands, and you are free to use any of them you like; see the Turtle module documentation.

Step 3

The first type of fractal we will examine uses a simple rewrite rule. The idea is to replace a straight line segment with four smaller line segments, each 1/3 the length of the original, as shown below.

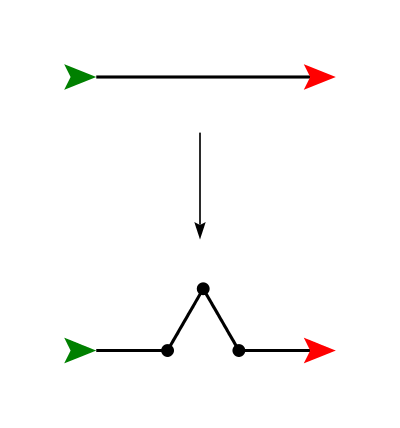
(Note that the angles are 60 and 120 degrees; the green turtle shows where the turtle starts and the red turtle shows where it ends.) If we repeat this replacement operation, again replacing each of the four line segments, we obtain something like this:

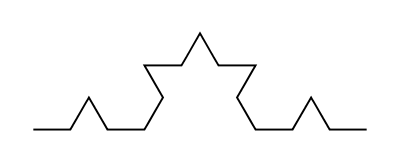
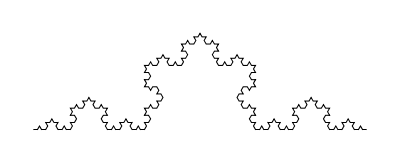
Continuing to repeat this process yields an ever more detailed "snowflake" curve. For example, here is the result after iterating 4 times:

In a file called fractal.py, type in the following recursive function:

import turtle

def koch(t, n, size):
    if n == 0:
        t.forward(size)
    else:
        koch(t, n - 1, size / 3)
        t.left(60)
        koch(t, n - 1, size / 3)
        t.right(120)
        koch(t, n - 1, size / 3)
        t.left(60)
        koch(t, n - 1, size / 3)

This function uses the turtle object t to draw an order-n Koch curve, that is, the result of iterating this process n times. In the base case (when n == 0), it simply draws a line of length size; in the recursive case, it draws four smaller copies of an order-(n - 1) Koch curve, arranged as shown in the replacement rule above.

Once you have typed in the function, test it using this function:

def koch_tester():
    t = turtle.Turtle()
    t.speed(10)
    for i in range(1, 5):
        t.penup()
        t.goto(0, 100 * (i - 2))
        t.pendown()
        koch(t, i, 100)

Step 5

Try your recursive coding skills out with curves generated by the replacement shown below. Write a function called koch2(t, n, size) that draws the Koch 2 fractal.

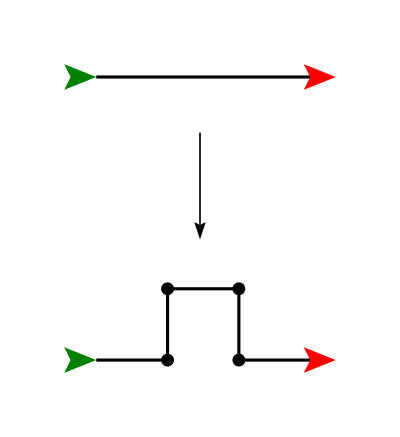
Step 6

Now do the same thing for the following replacements:

Write a function called koch3(t, n, size) that draws the Koch 3 fractal.

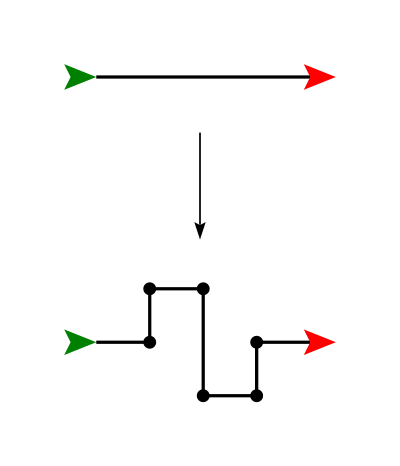
Note that in the middle of the above replacement pattern there is a long vertical segment. This can either be replaced by a single half-sized copy, or by two quarter-sized copies. These different methods yield different (but related) fractals. Use whichever one you like better! For the C-curve below, however, the bottom segment really does need two half-size copies (hence the dot in the middle), instead of a single full-size copy; otherwise it will look pretty boring.

Write a function called c_curve(t, n, size) that draws the C-curve fractal.

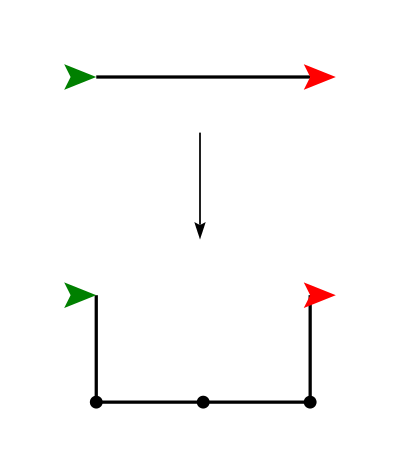
Note the direction the turtle is facing at the beginning and end of the replacement above!

Step 7

These next two are a little different. They each require two functions for replacement instead of just one above. The first function is indicated by blue lines, and the second function by orange lines. (The color simply distinguishes the functions; you do not need to draw colored lines.)

Dragon Curve

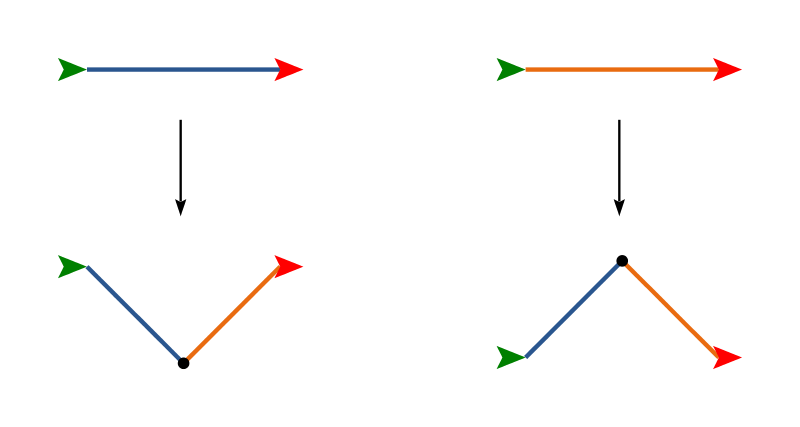
Note that the above replacements are drawn to scale: the distance between the start and end points are the same. The blue and orange lines make a right angle. You should think about the question: what should be the length of the blue and orange lines at the bottom (after replacement), relative to the length of the lines at the top (before replacement)?

Sierpinski's Triangle

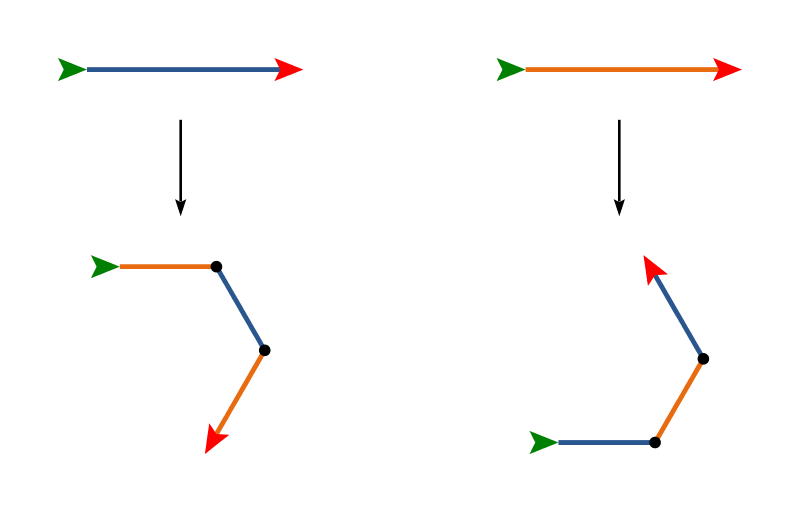
This one is a bit strange since the turtle ends up facing in a different direction after the replacement. Just go with it! Also, for this one, don't worry too much about the relative lengths (though it is a fun geometry challenge to figure out the right values to make the fractal stay the same size with different numbers of iterations).

Step 8

Create your own replacement rule for your personal fractal, and write code to draw it! In your Lab Evaluation Document, describe what you expected to happen when you planned your fractal, and discuss how your expectations were (or were not) met after it executed.

What to Hand In

Log in to Moodle and turn in your code. Make sure you have followed the Python Style Guide, and have run your project through the Automated Style Checker.

You must hand in:

fractal.py
Lab Evaluation Document

Grading

To earn a D on this lab, complete Steps 1 and 2.
To earn a C on this lab, do the above and complete Step 3.
To earn a B on this lab, do the above and complete Steps 5 and 6.
To earn a A on this lab, do the above and complete Step 7.
To earn a 100 on this lab, do the above and complete Step 8.

CSCI 150 - Lab 8Fractal Recursion