CSCI 151 Lab 13: Learning to Play Tic Tac Toe

Overview

In this lab, we will implement a HashTable for use in a learning algorithm for Tic Tac Toe.

Setup

Description

HashTables are an efficient implementation of the Map interface, with the ability to lookup items in constant time on average. For this lab, we will be implementing a HashTable to be used in the context of an Artificial Intelligence game player.

In particular, we will be learning how to play the game TicTacToe. After a game is played, each board state along the path from the initial board to the final board will be recorded as a win for the winning player. If the board state has never been encountered before, then a new entry is created in a HashTable with equal win/loss/draw counts, and then updated based on this play. Later board states will be influenced more than earlier board states, to account for the recency of the position and opportunity for alternate play choices.

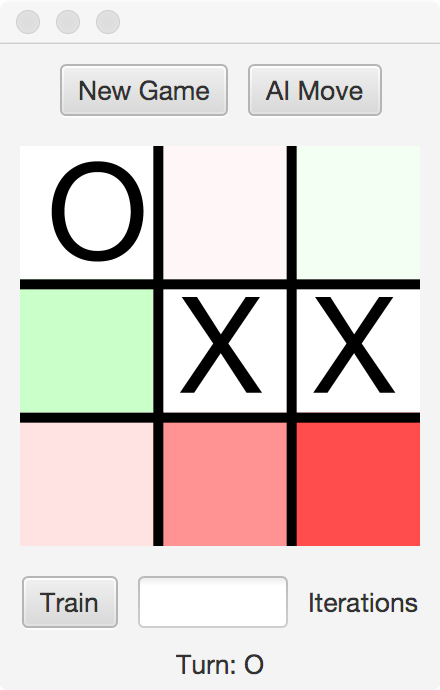
As more games are recorded, the AI will build up a probabilistic picture of the game tree. The user can elect to train multiple iterations at once with the Train button, which will play random games of the computer vs itself. Using the learned knowledge, the AI Move button will select the move that has shown the highest probability of success.

Besides the HashTable to store board states, another HashTable is used to record a GUI Rectangle for each position on the board. To guide the player, those moves more likely than average to succeed will be shaded green, while those less likely to succeed will be shaded red.

In your code below, you should follow good coding practices, for example, noticing when you are writing essentially the same code twice and abstracting this pattern into a private method.

Step 1: put (D)

The first method we must implement for the HashTable is the put method. When passed a key-value pair, first, the associated index into the allocated array must be found using the hashCode() of the key modded by the length of the array. (Use Math.floorMod instead of %, since it deals correctly with negative numbers.)

If there is no entry at the found location, a new HashNode is created to store the key and value. However, if there already exists a HashNode at that location, we first check to see if the keys match. If a match is found, the new value replaces the old value for that node. If the keys do not match, then a collision has occurred and must be resolved. You can either use linear probing to incrementally walk the array looking for either a matching key or an open spot to add a new HashNode, or sequential chaining to walk the linked list of HashNodes at that location, looking for either a matching key or the end of the chain where a new HashNode can be added. Only when a new HashNode is created should the size counter be incremented.

When the load factor of the HashTable, determined by the size of the HashTable divided by the capacity of the array, exceeds 0.75, the put method should double the size of the array and reput all the entries into the new array.

Step 2: get (C)

This method finds the associated index into the allocated array using the hashCode() of the key modded by the length of the array. Then, according to the collision resolution method you chose above, we walk through the HashNodes found, until either a matching key is identified and the method returns the value of this node, or we encounter a null position and the method returns null.

Step 3: containsKey (B)

This method finds the associated index into the allocated array using the hashCode() of the key modded by the length of the array. Then, according to the collision resolution method you chose above, we walk through the HashNodes found, until either a matching key is identified and the method returns true, or we encounter a null position and the method returns false. (Warning: don’t copy and paste code! Figure out how to abstract common code into private helper methods.)

Step 4: allKeys (A)

While the keys cannot be returned in order using a hash table, it is feasible to loop through the array and collect all the keys in this unordered fashion. Note that if you chose to implement sequential chaining, that you must collect all the keys in the linked list, not just the key of the first element. Store each key when found in an ArrayList, and return this list.

Grading

© Mark Goadrich, Hendrix College