CSCI 151 Lab 7: The Two Towers

Overview

This lab will:

Give you practice writing and using Iterators.
Give you practice working with integers as sequences of bits.

Acknowledgements

This lab is adapted from Java Structures by Duane A. Bailey.

Introduction

Suppose that we are given \(n\) uniquely sized cubic blocks and that each block has a face area between \(1\) and \(n\) square inches. If we build two towers by stacking these blocks, how close can we get their heights? The following two towers built by stacking 15 blocks, for example, differ in height by only 129 millionths of an inch:

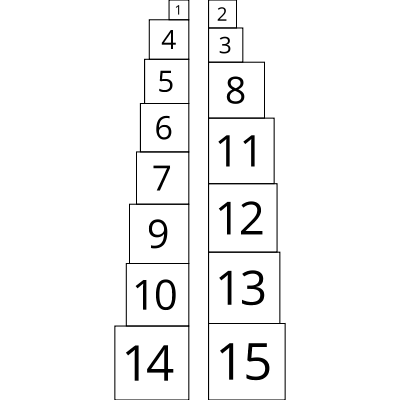
Still, this stacking is only the second-best solution! To find the best stacking, we could consider all the possible configurations. We do know one thing: the total height of the two towers is computed by summing the heights of all the blocks:

\[h = \sum_{i=1}^n \sqrt i\]

If we consider all the subsets of the \(n\) blocks, we can think of the subset as the set of blocks that make up, say, the left tower. We only need to keep track of which subset comes closest to \(h/2\) without exceeding it. In this lab, we will represent a set of \(n\) distinct objects by an ArrayList, and we will construct an Iterator that returns each of the \(2^n\) subsets.

Background

The trick to understanding how to generate a subset of \(n\) values from an ArrayList is to first consider how to generate a subset of indices of elements from \(0\) to \(n-1\). Once this simpler problem is solved, we can use the indices to help us build an ArrayList (or subset) of values identified by the indices.

There are exactly \(2^n\) subsets of values \(0\) to \(n-1\). We can see this by imagining that a coin is tossed \(n\) times—once for each value—and the value is added to the subset if the coin flip shows a head. Since there are \(2 \times 2 \times \dots \times 2 = 2^n\) different sequences of coin tosses, there are \(2^n\) different subsets.

We can also think of the coin tosses as determining the values for \(n\) different digits in a binary number. The \(2^n\) different sequences generate binary numbers in the range \(0\) through \(2^n - 1\). Given this, we can see a line of attack: count from \(0\) to \(2^n - 1\) and use the binary digits (bits) of the number to determine which of the original values of the ArrayList are to be included in a subset. For example, suppose our original ArrayList contains \(3\) items. Then the counter \(0 = 000_2\) means the empty subset; \(3 = 011_2\) means the subset containing only the first and second items but not the third, since the first two bits (counting from the right end!) of \(011_2\) are \(1\), but the third bit is \(0\).

Computer scientists work with binary numbers frequently, so there are a number of useful things to remember:

An int value is represented by 32 bits. A long is represented by 64 bits. For maximum flexibility, it will be useful to use long integers to represent sets of up to 64 elements.
The arithmetic left shift operator << can be used to quickly compute powers of \(2\). Left shift works by “shifting” the bits of a value over, adding zero bits on the end. For example, \(1101_2 <\!\!< 1 = 11010_2\); \(1101_2 <\!\!< 2 = 110100_2\); \(1101_2 <\!\!< 3 = 1101000_2\); and so on. Just as adding a zero to the end of a decimal number means multiplying by ten, adding a zero to the end of a binary number is the same as multiplying by \(2\). Therefore, the value \(2^i\) can be computed by starting with a single \(1\) bit, and shifting it \(i\) places to the left. In Java we write this 1L << i. The constant 1L is the value one stored as a 64-bit long value. Using this constant ensures that we are using a 64 -bit shift operation resulting in a long value instead of a 32-bit operation resulting in an int value.
The “bitwise AND” of two numbers (written & in Java) takes the logical AND of each pair of bits. For example, 101110 & 110100 = 100100. Each bit in the result is 1 only if both inputs to & had a 1 bit in the corresponding place; otherwise the result bit will be 0.

We can use this to determine the value of a single bit in a number’s binary representation: to retrieve bit \(i\) of a long integer m, we first compute \(2^i\) using 1L << i. This creates a binary number with all zero bits except for a single 1 bit at index i. If we then take the bitwise AND of this with m (that is, m & (1L << i)), all the bits of the result are zero except possibly bit i: in particular, the result is \(0\) if m had a \(0\) bit at position i, and nonzero otherwise.

Step 1: SubsetIterator

Create a new SubsetIterator<E> class which implements Iterator<ArrayList<E>>. This new class should have a constructor that takes an ArrayList<E> as its sole argument. Subsets of this ArrayList will be returned as the Iterator progresses. Notice that the class implements Iterator<ArrayList<E>>, not Iterator<E>!

Internally, SubsetIterator should use a long value to represent the current subset. This value starts out as \(0\) (which represents the empty set) and increases to \(2^n - 1\) (which represents the entire set of values) as the Iterator progresses.

Write a hasNext method that returns true if the current value is a reasonable representation of a subset.

Write a next method that returns a new ArrayList of values that are part of the current subset (using the techniques explained in the Background section above), and then increments the counter. If bit \(i\) of the current counter is 1, element \(i\) of the original ArrayList should be included in the resulting subset ArrayList .

Step 2: Test

You can now test your new SubsetIterator by having it print all the subsets of an ArrayList of values. For example, write a main method for your SubsetIterator that creates an ArrayList with the Integers from 0 through 3, creates a SubsetIterator with this ArrayList, and then prints out all subsets returned. Make sure you end up with all \(16\) different subsets printed.

Step 3: Best height

To solve the two towers problem, write a main method in a new class TwoTowers that inserts the values \(\sqrt 1, \sqrt 2, \dots, \sqrt n\) into an ArrayList<Double>. (To compute the square root of n, you can use the Math.sqrt(n) method.) A SubsetIterator is then used to construct \(2^n\) subsets of these values. The values of each subset are summed, and the sum that comes closest to, but does not exceed, the value \(h/2\) is remembered. After all the subsets have been considered, print the height of the tower that came closest to \(h/2\).

Step 4: Best tower

Your solution from step 3 printed out the height of the best tower, but we want to actually know which blocks to use! Modify your code so that it prints out not just the height of the best tower, but the numbers of the blocks that were used to make it. (Hint: change your ArrayList<Double> to an ArrayList<Integer>.)

Thought Questions

What is the best solution to the \(15\)-block problem?
How long does it take your program to find the answer to the \(20\)-block problem? (You may find the StopwatchCPU or NanoStopwatch classes from a previous lab to be helpful.) Based on the time taken to solve the 20-block problem, about how long do you expect it would take to solve the 21-block problem? What is the actual time? How about the 25-block problem? Do these agree with your expectations, given the time complexity of the problem? What about the 40- and 50-block problems? (These will take a very long time. Just estimate based on the run times of the smaller problems).
This method of exhaustively checking the subsets of blocks will not work for very large problems. Consider, for example, the problem with \(50\) blocks: there are \(2^{50}\) different subsets. One approach is to repeatedly pick and evaluate random subsets of blocks; stop the computation after 1 second of elapsed time, printing the best subset found so far. How would you implement randomSubset, a new SubsetIterator method that returns a random subset? (You do not have to actually implement it, just describe how you would implement it.)

What to Hand In

You should turn in

SubsetIterator.java
TwoTowers.java
A document containing your answers to the Thought Questions

Grading

To get a C, complete Steps 1 and 2 (SubsetIterator + test)
To get a B, complete Step 3 (Best height)
To get an A, complete Step 4 (Best tower)
To get a 100, complete all the steps and the Thought Questions