• Back to main page

Project 3: Quilt

let swirl = (let grate = -cos (x*20*pi)/2 + 0.5 in grate @ (20*(sin(50*sqrt(x*x + y*y)))))
in  swirl * yellow + (y+1)/2 * blue

In this project, you will create a language which can describe and produce images like the one above!

Getting started

• Download the starter code and unzip it in a directory.

• You should be able to compile and run the project with stack build stack exec quilt

• You will mostly be adding code to Quilt.hs, although you may also customize the messages defined in QuiltREPL.hs.

• If you like, you can also view the source for this project description file itself, although it is not necessary: QuiltProject.lhs.

The Quilt language: basic examples

The basic Quilt language has real numbers, booleans, arithmetic operations, if-expressions, names of standard colors, RGB color expressions, and quilt expressions.

The name of a color by itself produces an image consisting entirely of that color:

red

Arithmetic can be done on colors, which results in their red, green, and blue channels being operated on componentwise.

red + blue

Colors can be explicitly constructed by giving a triple of values in list notation. Each channel should be a number between 0 and 1; [0,0,0] represents black and [1,1,1] white.

[0.2, 0.8, 0.5]

To make things more interesting, there are special reserved variables x and y which can be used to refer to the position within the image. All the images are centered at the origin, with x and y ranging from \(-1\) to \(1\). As a simple example, we can use if together with x and y to choose different colors for different parts of the image.

if x < y then red else blue

We can also use x and y in more continuous ways. For example, this image smoothly interpolates between red and blue, using the value of x.

(x+1)/2*red + (1-(x+1)/2)*blue

We could also use x and y inside a color expression, as a more direct way to produce smoothly varying colors.

[(x+1)/2, (y+1)/2, 0.5]

Finally, the quilt operator takes four images and arranges them in a square.

quilt 0.4 yellow red (quilt green orange blue purple)

Notice how the number 0.4 can be used as a color, resulting in the color [0.4, 0.4, 0.4] (a dark gray).

Grammar

More explicitly, the basic Quilt language has the following grammar:

<colorlit> ::= 'red' | 'orange' | 'yellow' | ...
<num>      ::= integer or floating-point
<coord>    ::= 'x' | 'y'
<bool>     ::= 'False' | 'True'

<qexp> ::=
  | <colorlit>
  | <num>
  | <coord>
  | <bool>
  | '[' <qexp> ',' <qexp> ',' <qexp> ']'
  | 'if' <qexp> 'then' <qexp> 'else' <qexp>
  | <uop> <qexp>
  | <qexp> <bop> <qexp>
  | 'quilt' <qexp> <qexp> <qexp> <qexp>

<uop>        ::= '-' | '!'
<bop>        ::= <arith> | <comparison> | <boolean>
<arith>      ::= '+' | '-' | '*' | '/'
<comparison> ::= '<' | '>' | ...
<boolean>    ::= '&&' | '||'

Types

Quilt has three types: booleans, floating-point numbers, and colors. Note that a “color” is really a triple of arbitrary floating-point numbers; it does not necessarily have to be a valid, visible color. For example, [0.2,0.3,-1] is a “color” even though an actual visible color must have three values between 0 and 1.

• <colorlit> values have type color; numeric values have type number, as do <coord>s; booleans literals have type boolean.
• if-expressions expect a boolean test, and two cases with the same type.
• Literal color triples expect three numeric values, and produce a color.
• Boolean operators like !, &&, etc. expect booleans and yield booleans.
• Comparison operators expect two numeric values and yield a boolean; it does not make sense to compare colors.
• Arithmetic operators are overloaded to work on either numbers or colors. Doing arithmetic on colors results in the arithmetic being done componentwise. For example, [0.2, 3, -1] * [6, 2, 3] = [1.2, 6, -3].
• quilt is overloaded to work on any type. For example, it can take four boolean expressions and construct a new boolean expression; or four numeric expressions to construct a numeric expression, and so on. (You might be confused at this point: how can quilt produce a single number or color? The answer is that it doesn’t: the fact that its type is, say, a color does not mean it produces a single color, but rather that it produces a (possibly different) color at every \((x,y)\) coordinate.)

There is one final twist: numbers are a subtype of colors, that is, a numeric value can be used anywhere that a color is expected. (As we have seen, the number \(n\) will be interpreted as the color \([n,n,n]\).) This has some interesting implications. For example:

• Arithmetic operators do not literally require two arguments of the same type. One can be a number and the other a color, in which case the number will be automatically treated like a color (for example, 0.1 + [0.2, 0.3, 0.5] = [0.3, 0.4, 0.6]). If the two arguments to an arithmetic operator are both numbers, then the result is still a number; but if either argument is a color, then the result will be a color.

• The two branches of an if do not have to be the same if one is a number and one a color. This works similarly to arithmetic operators.

• quilt expects four expressions of the same type—four booleans, four numbers, or four colors. But since numbers can be used as colors, it should be possible to give quilt any combination of numbers and colors. If quilt is given four booleans, the whole expression has type boolean; if given four numbers, the whole expression has type number; if given a mixture of numbers and colors, the whole expression has type color.

Some hints for dealing with subtyping in your type checker:

• You may find it helpful to write a function like isSubtype :: Type -> Type -> Bool. Note that every type is a subtype of itself.

• Try to separate type inference involving subtyping into two phases: first, recursively infer the types of subexpressions; second, make sure their types are appropriately compatible, and if so compute an appropriate output type. You will probably want one or more helper functions to do this.

Semantics

The x and y coordinates for an image produced by the Quilt language will both vary from -1 to 1, with the origin (0,0) in the center of the image.

Everything in the quilt language (booleans, numbers, colors) can vary continuously over 2D space. For example, consider the expression x < y: x and y both have type number, so x < y has type boolean. However, semantically it does not represent just a single boolean, but rather a function of type Double -> Double -> Bool which attaches a boolean value to every point in 2D space (according to whether the x-coordinate at that point is less than the y-coordinate). If you look again at other examples above, you will see more examples of numbers and colors varying over space.

This means your interpreter should always produce something of the form (Double -> Double -> ...). One could have it produce a Double -> Double -> Value, and define a new type Value which can be either a boolean, a number, or a color. However, since Quilt expressions will be typechecked, you can use the same trick we have used before: just represent everything (booleans, numbers, and colors) as a Color, that is, a list of Double values. So your interpreter will always output a QuiltFun, that is, a Double -> Double -> Color. A boolean can be represented by, say, [0] or [1]; a number n should be represented by the list [n,n,n]. If you have a [Double] but need a boolean or a number, just get the first element of the list. This way, your interpreter does not actually have to worry about issues of subtyping or conversion, and it does not need to do any pattern-matching to figure out what kind of value it has.

Basic assignment

The basic assignment is to get the Quilt language as described above working in the context of the provided REPL. The user enters an expression, and is shown a syntax error, a type error, or gets an image. Make sure your error messages are pleasant to read (e.g. using some sort of pretty-printing as appropriate) and informative. Here is an example interactive session with my implementation:

> 3 + True
Expressions 3 and True have incompatible types (number and boolean).
> [[5, 6, (8*9)+2], 0, 1]
Type mismatch: expression [5, 6, 8 * 9 + 2] was expected to be a number, but is actually a color.
> 3 + if
(line 1, column 7):
unexpected end of input
expecting end of "if", "(", "red", "orange", "yellow", "green", "blue", "purple", ...
> red + blue
256x256 -> quilt.png

Your project doesn’t need to look the same or have the same error messages as mine; I provide it simply for inspiration.

The maximum grade for completing just the basic assignment is a C.

What to turn in

• Of course you should turn in Quilt.hs. Be sure it has comments explaining the different pieces of your implementation, as appropriate.

• You must also turn in a file called README.txt. This file should contain:

  • Your name
  • A description of your implementation of Quilt and any extensions you added (see below)
  • A list of example Quilt expressions which show off the features of your language

• Turn in QuiltREPL.hs only if you made any modifications to it. If you did not modify it at all, you do not need to turn it in.

Extensions

The maximum grade for completing the basic assignment plus two extensions is a B; to earn an A, you must implement at least four extensions, at least one of which is not in the list below. Below I have listed a number of suggested extensions, but these are just suggestions: you should feel free to be creative and come up with your own. Feel free to consult with me if you are unsure whether your idea for an extension is feasible or substantive enough.

• Add more arithmetic functions such as sin, cos, exp, floor, ceil, round, sqrt, abs, more operators like % and ^, and so on. (Hint: parse functions like sin as prefix operators with high precedence in the expression parser.) (Hint: if you add trig functions, it’s nice to also add the constant pi.)

  

  (-cos(8*pi*x)/2 + 0.5) * green

  

  -cos(50*sqrt(x*x + y*y))/4 + -cos(50*(sqrt((x-0.2)*(x-0.2) + y*y)))/4 + 0.5

• Add variables and let-expressions. This extension has high bang for the buck, since it allows you to concisely describe much more complicated images by giving subpieces names and then being able to repeat them.

  

  let circ = 1-(x*x + y*y) in quilt [circ,0,0] [0,circ,0] [0,0,circ] circ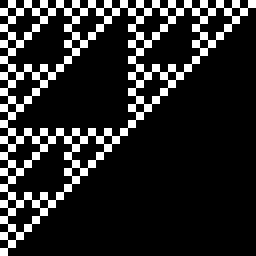

  

  let checks  = quilt black white white black in
  let checks2 = quilt checks checks checks black in
  let checks3 = quilt checks2 checks2 checks2 black in
  let checks4 = quilt checks3 checks3 checks3 black in
  let checks5 = quilt checks4 checks4 checks4 black in
  checks5

• Add operators to do geometric transformations like rotation, translation, and scaling. For example, you might add binary operators like
  • rot or @: rotation by an angle
  • tx: translate in the x direction
  • ty: translate in the y direction
  • scale: scale by a given factor
  • sx: scale in the x direction
  • sy: scale in the y direction

  Each of these binary operators takes an arbitrary type t as its first argument and a number as its second argument, and produces a result of type t.

  

  let circ = 1-(x*x + y*y) in
    ((circ*red) sx 0.6 tx 0.5)
    + ((circ*green) sy 1.1 ty 0.2)
    + ((circ*blue) scale 0.7 tx (-0.4))

  Really weird and cool things happen when you realize that you can transform by a “number” which actually varies over the plane! For example, here I make a grate consisting of vertical bars, and then apply a rotation of 40*(0.5-(x*x + y*y)) degrees at location (x,y):

  

  let grate = -cos (x*20*pi)/2 + 0.5 in grate @ (40*(0.5-(x*x + y*y)))

  I used a similar principle in constructing the example at the very top of this page. Note my rotations are specified in degrees, so the interpreter has to convert them to radians before giving them as arguments to sin and cos. You are free to use degrees, radians, fractions of a circle, or whatever other units you wish.

• Add a time dimension in order to create animations. For example, you can add another special variable t representing time, and change your interpreter so it now returns a function that expects three Double arguments (time, x, and y). The variable t allows you to describe arbitrary images that change over time. For example,

  (1-t) * blue + t * red

  might describe an animation which smoothly shifts from blue to red over the course of 1 second.

  If you want to do this extension, I can provide you with some Haskell code to turn such functions into animated GIF images.

• Add a fourth component to your colors in order to specify an alpha, i.e. transparency channel. Most likely, however, you will want to retain the ability to describe normal, opaque colors as well, so you will want a bit of subtyping magic, e.g. perhaps [0.1, 0.2, 0.3] is automatically treated as if it were [0.1, 0.2, 0.3, 0].

• Add complex numbers. For example, you can add a special constant i as well as a variable z which has the value x + i*y. This extension is interesting from a typing point of view: probably you would want a new type for complex numbers, with real numbers as a subtype. Some functions such as abs and the arithmetic operators work on both real and complex numbers; but some things like comparisons can only be done on reals, and colors can only be created from real numbers.

  Mumble mumble Möbius transforms something something mumble?

• Once you have added let-expressions and geometric scaling, you could try making let-expressions recursive (i.e. let x = q1 in q2 binds x in q1 as well as q2), in order to be able to produce fractal images. This can easily lead to infinite recursion, so you will have to add something to your interpreter to keep track of the current scaling factor, so it can cut off the recursion when the scaling factor gets sufficiently small (i.e. when further recursion would produce details smaller than one pixel).

• Add functions and function types. This is nontrivial but results in a much more expressive language. For example, instead of just giving individual images a name, you can give names to common operations on images and apply them multiple times.